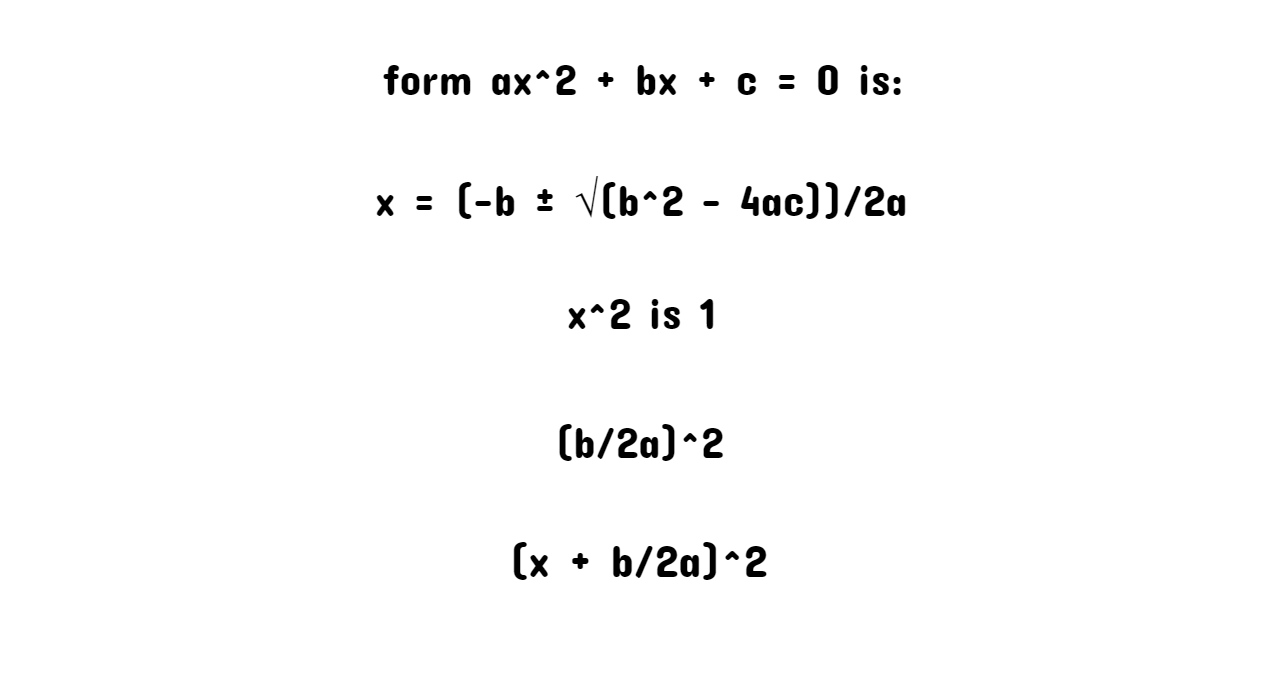How To Complete The Square Formula. The formula to complete the square for a quadratic equation of the form ax^2 + bx + c = 0 is:
x = (-b ± √(b^2 – 4ac))/2a
This formula gives the solutions for the quadratic equation by using the process of complete. To use this formula, you need to first convert the quadratic equation into standard form by moving the constant term to the right side of the equation, if necessary, and dividing both sides by the leading coefficient, so that the coefficient of x^2 is 1.
Learn More: How To Complete The Square
Then, to complete the square, you need to add and subtract (b/2a)^2 to the left side of the equation. This creates a perfect square trinomial that can be factored as (x + b/2a)^2.
Taking the square root of both sides and simplifying yields the formula above. The formula gives the two solutions to the quadratic equation, one with a plus sign and one with a minus sign in front of the square root.
Note that this formula may not work if the discriminant, b^2 – 4ac, is negative, which indicates that the quadratic equation has no real solutions. In that case, you would need to use the complex number system to find the solutions.
FAQ
How To Complete The Square Formula?
Form ax^2 + bx + c = 0 is:
x = (-b ± √(b^2 – 4ac))/2a
x = (-b ± √(b^2 - 4ac))/2a
" } } ] }