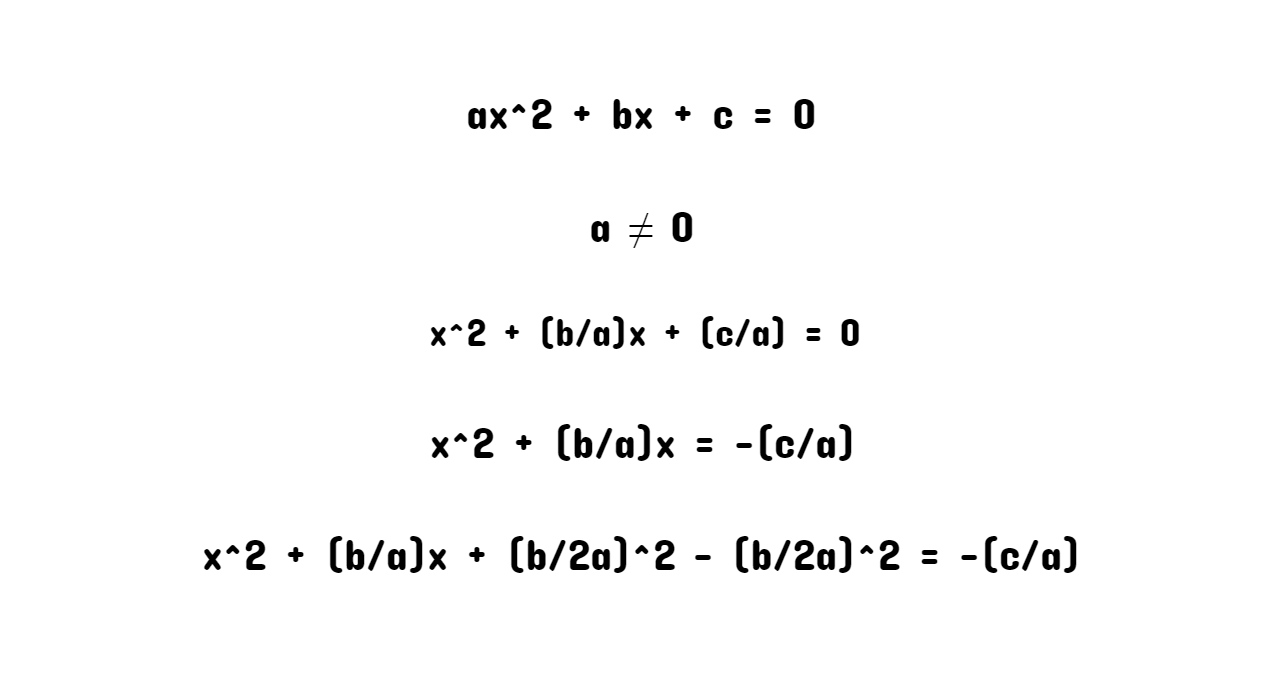How To Complete The Square. Completing the square a technique used in algebra to rewrite quadratic equations in a more useful form.The process involves adding and subtracting a constant term to create a perfect square trinomial.
How To Complete The Square
Here are the steps to complete the square:
- Start with a quadratic equation in the standard form: ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0.
- Divide both sides of the equation by a, if necessary, to make the coefficient of x^2 equal to 1: x^2 + (b/a)x + (c/a) = 0
- Move the constant term, (c/a), to the right side of the equation: x^2 + (b/a)x = -(c/a)
- Add and subtract (b/2a)^2 to the left side of the equation: x^2 + (b/a)x + (b/2a)^2 – (b/2a)^2 = -(c/a)
Learn More: How To Find All Eggs In Anime Adventures
- Simplify the left side of the equation: (x + b/2a)^2 – (b/2a)^2 = -(c/a)
- Take the square root of both sides of the equation: x + b/2a = ±√(-(c/a) + (b/2a)^2)
- Subtract b/2a from both sides of the equation: x = (-b ± √(b^2 – 4ac))/2a
- Simplify the right side of the equation to get the solutions to the quadratic equation.
So, by following these steps, you can complete the square of any quadratic equation and solve it to find the solutions of the equation.
A perfect square trinomial a trinomial expression that can be written as the square of a binomial.
FAQ
How To Complete The Square?
Here are the steps to complete the square:
- Start with a quadratic equation in the standard form: ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0.
- Divide both sides of the equation by a, if necessary, to make the coefficient of x^2 equal to 1: x^2 + (b/a)x + (c/a) = 0
- Move the constant term, (c/a), to the right side of the equation: x^2 + (b/a)x = -(c/a)
- Add and subtract (b/2a)^2 to the left side of the equation: x^2 + (b/a)x + (b/2a)^2 – (b/2a)^2 = -(c/a)
- Simplify the left side of the equation: (x + b/2a)^2 – (b/2a)^2 = -(c/a)
- Take the square root of both sides of the equation: x + b/2a = ±√(-(c/a) + (b/2a)^2)
- Subtract b/2a from both sides of the equation: x = (-b ± √(b^2 – 4ac))/2a
- Simplify the right side of the equation to get the solutions to the quadratic equation.
- Start with a quadratic equation in the standard form: ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0.
- Divide both sides of the equation by a, if necessary, to make the coefficient of x^2 equal to 1: x^2 + (b/a)x + (c/a) = 0
- Move the constant term, (c/a), to the right side of the equation: x^2 + (b/a)x = -(c/a)
- Add and subtract (b/2a)^2 to the left side of the equation: x^2 + (b/a)x + (b/2a)^2 - (b/2a)^2 = -(c/a)
- Simplify the left side of the equation: (x + b/2a)^2 - (b/2a)^2 = -(c/a)
- Take the square root of both sides of the equation: x + b/2a = ±√(-(c/a) + (b/2a)^2)
- Subtract b/2a from both sides of the equation: x = (-b ± √(b^2 - 4ac))/2a
- Simplify the right side of the equation to get the solutions to the quadratic equation.